Well, can you?
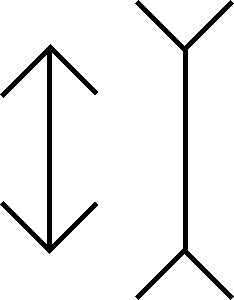
Muller-Lyer Illusion - are the long lines the same length?
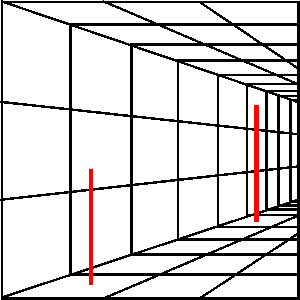
What about the two red lines in this image?

Look at the black centre of this image.
What happens to the grey area surrounding it ?
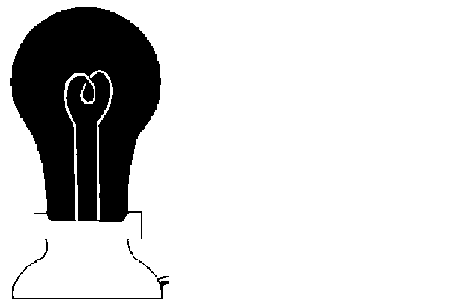
Look at the bulb for 30 seconds, then at the white area to the right.
The bulb will switch itself on!

Look at this image for 5 seconds, close your eyes and look at the white area
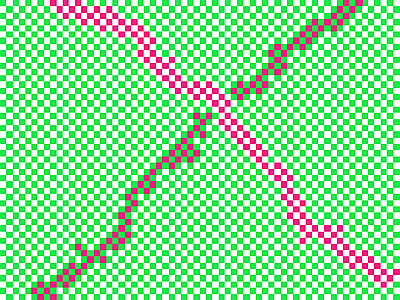
How many shades of pink are there in this picture ?
In fact there is only one!
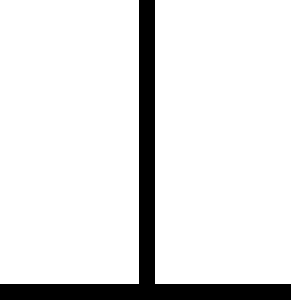
What about this pair of lines?
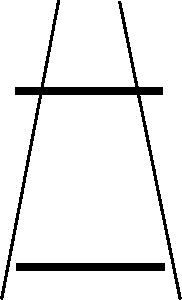
And this pair of thick lines?
First noted by Mario Ponzo in 1913

Perspective Distortion
The further the figure gets from us the bigger he gets?
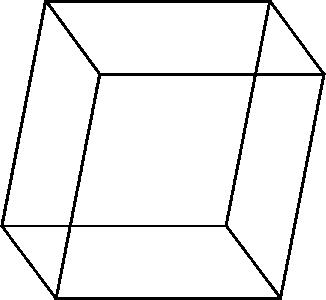
Necker Cube ~ 1832
Which face is nearer to you?
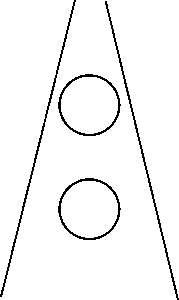
Ponzo Illusion
Which circle is bigger? or are they the same size?
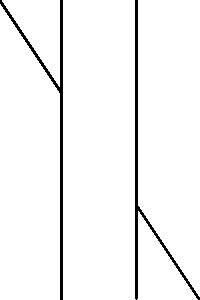
Poggendorff Illusion
Would the inclined line make a single straight line?
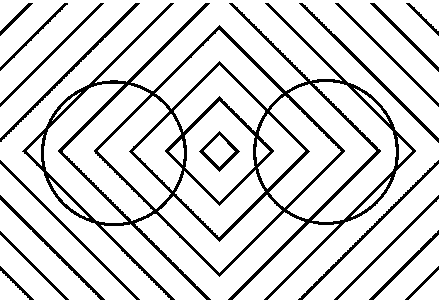
Orbison Variant
Are these true circles?
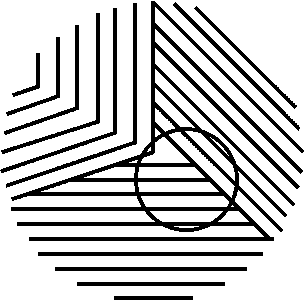
Another Orbison variant - is this really a circle ?
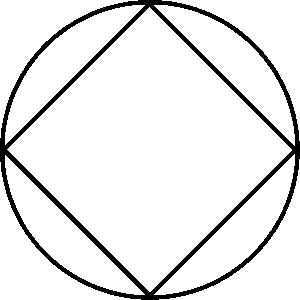
Lipps Variant A
What is that diamond doing to that circle?
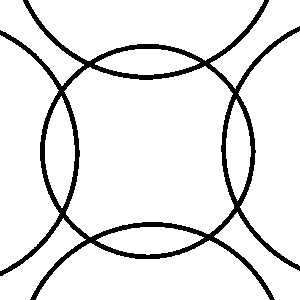
Lipps Variant B
What are the arcs doing to the circle?

Are the shades of grey different or the same?

Which of these two shapes is the larger?