

HomePage | Optical Illusions | War Stories | QBasic | Dads Navy Days | Bristol | Bristol, USA | Bristol, Canada | Terre Haute | Miscellany | Web Stuff | About Ray | Site Map | Site Search | Messages | Credits | Links | Web Rings
QBasic | Errors | 40lb Weight | Bits | Chance | Colours | Dates | Delays | File Dialog | Files | Input | Matching | Menus | Mouse | Numbers | SeqNo | SIRDS | Sorts | Text | Timer | DLoads
My wife likes mathematics. She's got a MS in it, she teaches it at degree level and one of her pastimes is solving mathematical puzzles. This page is dedicated to her. Having said that, any mistakes in the programs on this page are all my fault.
"Well, if I called the wrong number, why did you answer?" James Thurber, New Yorker, June 5th 1937.
PI :-
Oddly enough there isn't a built in constant for PI, but it's easily calculated yourself. You can define a number variable as a SINGLE or LONG and use ATN(1) * 4
For example using
DIM PI AS SINGLE
PI = ATN(1) * 4
will give PI as 3.141593, using
DIM PI AS DOUBLE
PI = ATN(1) * 4
will give PI as 3.141592653589793
nth Roots :-
QBasic hasn't a built in function for finding the nth root of a number, but it isn't too hard to find the nth root of any number yourself. This is due to the fact that the nth root of a number is the number raised to the (1/n) power
'nRoot.bas Ray Thomas April 2002
'The nth root of a number is the number raised to the (1/n) power:
DIM Num AS DOUBLE
DIM Root AS DOUBLE
DIM Count AS INTEGER
CLS
PRINT
INPUT "Please input the number you want the roots of"; Num
PRINT
PRINT " n", " nth root", , " nth root ^ n"
PRINT
FOR Count = 1 TO 10
Root = Num ^ (1 / Count)
PRINT Count, Root, Root ^ Count
NEXT Count
END
The program also demonstrates how errors creep into calculations, even when the numbers used are DIM'd as DOUBLES.
Number Bases :-
This program is able to convert from any number to any other number base. It has a flaw in it. Although the program can convert to any base number, I'm not sure what happens after Base 37, this is because after the decimal system in order to add the extra figures needed to the number series, A = 10, B = 11, C = 12 etc. I've no idea what happens after Z is reached, so I've left the program adding the characters from the ASCII table.
Q: Why do mathematicians often confuse Halloween and Christmas?
A: Because Oct 31 = Dec 25
To convert a decimal number to another base it's best to make a list of the powers of that base :-
... X10 , X9, X8, X7, X6, X5, X4, X3, X2, X1, X0
Any number to the power of 0 is 1, any number to the power of 1 is that number. For Base 3 the powers are :-
... 19683, 6561, 2187, 729, 243, 81, 27, 9, 3, 1
Say you want to see what 169 is to base 3, the largest number that can go into 169 is 81 which goes into it twice, remainder 7. 27 and 9 can't go into 7 so these positions become 0's. The next power that can go into 7 is 3, which goes into it twice, remainder 1. This means that 169 as Base 3 is 20021. What is happening is that we are doing a long division.
To change a number in a Base back to decimal we once again write the powers of that base and write the number beneath it. We then can then count off the number as a decimal.
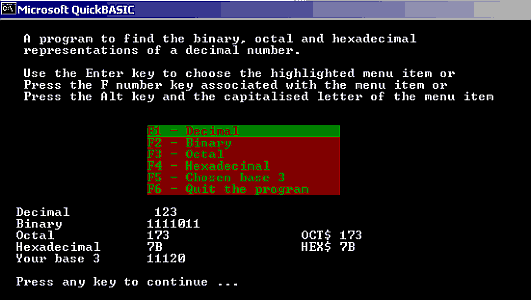
Screenshot of Numbase.bas
'NumBase Ray Thomas March 2002
OPTION BASE 1
'*** Calculation variables ***
DIM Bases(5) AS INTEGER 'Array to hold the base numbers
DIM NumArray(5) AS STRING 'Array to hold converted numbers
DIM UserNum AS DOUBLE 'User supplied number as decimal
DIM TempNum AS DOUBLE 'Temporary number variable
DIM BaseNum AS INTEGER 'Base to do the conversion to
DIM ModNum AS INTEGER 'Remainder from the calculations
DIM StrNum AS STRING 'Used to hold a number as a string
DIM Count AS INTEGER 'Loop counter
DIM OutNum AS DOUBLE 'Output from to Decimal routine
DIM Counter AS INTEGER 'Loop Counter
DIM PosnNum AS STRING 'Character at a position inside a string
DIM ConvNum AS INTEGER 'Numeric of PosNum
'*** Menu variables ***
DIM MenuItem(6) AS STRING * 25 'Define the menu item array
DIM ChooseItem AS INTEGER 'Currently chosen menu item
DIM XMenuposn AS INTEGER 'Controls the menu item X positions
DIM YMenuPosn AS INTEGER 'Controls the menu item Y positions
DIM EndMenu AS INTEGER 'F, Enter or Alt keys pressed
DATA 10,2,8,16
DATA F1 - Decimal, F2 - Binary, F3 - Octal
DATA F4 - Hexadecimal, F5 - Choose a base, F6 - Quit the program
ChooseItem = 1 'Starting point of highlighted menu item
XMenuposn = 20 'X starting point of menu
YMenuPosn = 10 'Y starting point of menu
'*** Fill the bases array ***
FOR Count = 1 TO 4
READ Bases(Count)
NEXT Count
'*** Fill the MenuItme Array ***
FOR Count = 1 TO UBOUND(MenuItem$)
READ MenuItem(Count)
NEXT Count
CLS
PRINT
PRINT " A program to find the binary, octal and hexadecimal"
PRINT " representations of a decimal number."
PRINT
PRINT " Use the Enter key to choose the highlighted menu item or"
PRINT " Press the F number key associated with the menu item or"
PRINT " Press the Alt key and the capitalised letter of the menu item"
GOSUB DrawMenu
'*** get cursor key movements and redraw menu ***
DO
DO
Cmmnd$ = (INKEY$)
IF LEN(Cmmnd$) = 2 THEN Cmmnd$ = RIGHT$(Cmmnd$, 1)
IF Cmmnd$ = "8" OR Cmmnd$ = CHR$(72) THEN GOSUB MoveUp
IF Cmmnd$ = "2" OR Cmmnd$ = CHR$(80) THEN GOSUB MoveDown
IF Cmmnd$ = "7" OR Cmmnd$ = CHR$(71) THEN ChooseItem = 1
IF Cmmnd$ = "1" OR Cmmnd$ = CHR$(79) THEN ChooseItem = UBOUND(MenuItem)
IF Cmmnd$ = CHR$(13) THEN EndMenu = 1
IF Cmmnd$ = CHR$(59) OR Cmmnd$ = CHR$(32) THEN
ChooseItem = 1
EndMenu = 1
END IF
IF Cmmnd$ = CHR$(60) OR Cmmnd$ = CHR$(48) THEN
ChooseItem = 2
EndMenu = 1
END IF
IF Cmmnd$ = CHR$(61) OR Cmmnd$ = CHR$(24) THEN
ChooseItem = 3
EndMenu = 1
END IF
IF Cmmnd$ = CHR$(62) OR Cmmnd$ = CHR$(35) THEN
ChooseItem = 4
EndMenu = 1
END IF
IF Cmmnd$ = CHR$(63) OR Cmmnd$ = CHR$(46) THEN
ChooseItem = 5
EndMenu = 1
END IF
IF Cmmnd$ = CHR$(64) OR Cmmnd$ = CHR$(16) THEN
ChooseItem = 6
EndMenu = 1
END IF
GOSUB DrawMenu
LOOP UNTIL EndMenu = 1
'*** Reset variables, there are problems if this is not done ***
FOR Count = 1 TO 5
NumArray$ = ""
NEXT Count
TempNum = 0
StrNum$ = ""
BaseNum = 0
ModNum = 0
UserNum = 0
EndMenu = 0
OutNum = 0
ConvNum = 0
EndMenu = 0
IF ChooseItem = 6 THEN EXIT DO
COLOR 7, 0
IF ChooseItem = 5 THEN
GOSUB GetBase
ELSE
GOSUB GetNumber
IF ChooseItem <> 1 THEN GOSUB ToDecimal
GOSUB ToBase
GOSUB Results
END IF
LOOP UNTIL ChooseItem = 6
END
DrawMenu:
'*** Draw the menu ***
LOCATE YMenuPosn, XMenuposn
FOR Count = 1 TO UBOUND(MenuItem$)
IF Count = ChooseItem THEN COLOR 4, 2 ELSE COLOR 2, 4
LOCATE CSRLIN, XMenuposn
PRINT MenuItem$(Count)
NEXT Count
RETURN
MoveUp:
IF ChooseItem = 1 THEN
ChooseItem = UBOUND(MenuItem$)
ELSE
ChooseItem = ChooseItem - 1
END IF
RETURN
MoveDown:
IF ChooseItem = UBOUND(MenuItem$) THEN
ChooseItem = 1
ELSE
ChooseItem = ChooseItem + 1
END IF
RETURN
ToBase:
'*** Do Decimal to other bases ***
'*** The code below will work for ANY base ***
'*** It needs the number as a numeric to work ***
FOR Count = 2 TO UBOUND(Bases)
IF Bases(Count) = 0 THEN EXIT FOR
TempNum = VAL(NumArray(1))
BaseNum = Bases(Count)
StrNum$ = ""
'*** Take the number, and keep dividing by the base number ***
'*** Add the results to the output string ***
DO
ModNum = TempNum MOD BaseNum
TempNum = FIX(TempNum / BaseNum)
IF ModNum > 9 THEN
StrNum$ = CHR$(ModNum + 55) + StrNum
ELSE
StrNum$ = STR$(ModNum) + StrNum$
END IF
StrNum$ = LTRIM$(RTRIM$(StrNum$))
IF TempNum < BaseNum THEN
IF TempNum > 9 THEN
StrNum$ = CHR$(TempNum + 55) + StrNum$
ELSE
StrNum$ = STR$(TempNum) + StrNum$
END IF
END IF
StrNum$ = LTRIM$(RTRIM$(StrNum$))
LOOP UNTIL TempNum < BaseNum
IF LEFT$(StrNum$, 1) = "0" THEN StrNum$ = MID$(StrNum$, 2)
NumArray(Count) = StrNum$
NEXT Count
RETURN
ToDecimal:
'*** Do Base to Decimal ***
'*** The code below will work for ANY base ***
'*** It needs the number as a string to work ***
BaseNum = Bases(ChooseItem)
StrNum$ = NumArray(ChooseItem)
FOR Count = 1 TO LEN(StrNum$)
'*** Convert the current character to a number ***
PosnNum$ = MID$(StrNum$, Count, 1)
IF ASC(PosnNum$) > 59 THEN
ConvNum = ASC(PosnNum$) - 55
ELSE
ConvNum = VAL(PosnNum)
END IF
'*** Get the value of that base at that position ***
'*** the series goes ... n^5, n^4, n^3, n^2, n, 1 ***
IF Count = LEN(StrNum$) THEN
TempNum = 1
ELSE
TempNum = BaseNum
FOR Counter = 1 TO (LEN(StrNum$) - Count - 1)
TempNum = TempNum * BaseNum
NEXT Counter
END IF
OutNum = OutNum + (TempNum * ConvNum)
NEXT Count
NumArray$(1) = LTRIM$(STR$(OutNum))
RETURN
GetBase:
LOCATE 17, 3
PRINT SPACE$(60)
LOCATE 17, 3
INPUT "What number base do you want to use ", UserNum
Bases(5) = UserNum
MenuItem$(5) = "F5 - Chosen base" + STR$(UserNum)
LOCATE 17, 3
PRINT SPACE$(60)
RETURN
GetNumber:
LOCATE 17, 3
PRINT SPACE$(60)
LOCATE 17, 3
INPUT "What number do you want to convert ", UserNum
NumArray(ChooseItem) = STR$(UserNum)
LOCATE 17, 3
PRINT SPACE$(60)
RETURN
Results:
LOCATE 17, 3
PRINT "Decimal"; TAB(20); NumArray$(1)
LOCATE 18, 3
PRINT "Binary"; TAB(20); NumArray$(2)
LOCATE 19, 3
PRINT "Octal"; TAB(20); NumArray$(3)
LOCATE 20, 3
PRINT "Hexadecimal"; TAB(20); NumArray$(4)
IF NumArray$(5) <> "" THEN
LOCATE 21, 3
PRINT "Your base"; Bases(5); TAB(20); NumArray$(5)
END IF
'*** Check the results ***
LOCATE 19, 40
PRINT "OCT$ "; OCT$(VAL(NumArray$(1)))
LOCATE 20, 40
PRINT "HEX$ "; HEX$(VAL(NumArray$(1)))
LOCATE 23, 3
PRINT "Press any key to continue ..."
DO
LOOP UNTIL INKEY$ <> ""
FOR Count = 17 TO 23
LOCATE Count, 3
PRINT SPACE$(60)
NEXT Count
RETURN
Number Series :-
Number series are fascinating. They take a simple concept and from that a whole series of numbers can be generated. Take Prime Numbers, the series starts off with the fact that some numbers are only divisible by themselves and 1. I've no idea what the largest prime number that has been so far calculated is, but, there is a class of prime numbers known as the Mersenne Primes. These take the form 2p - 1. In plain English, they are 2 to the power of a prime number - 1. As the Prime Number series runs 2, 3, 5, 7 ... the Mersenne Prime Number series runs 3, 7, 31, 127 ... The first in the series is 3 = 22 - 1, followed by 7 = (23) - 1 = (2 * 2* 2) - 1, then 31 = 25 - 1 = (2 * 2 * 2 * 2 * 2) - 1, followed by 127 = 27 - 1 = (2 * 2 * 2 * 2 * 2 * 2 * 2) - 1. The largest Mersenne Prime calculated so far is the 39th in the series and is 213,466,917-1 which I'm not going to put here as it's got over 4 MILLION digits. Want to earn yourself $100,000? Then calculate and prove a 10 MILLION digit prime number. The information on Mercenne Primes was taken from Mersenne Prime Search.
The number series I've included in the program, numser.bas, are Catalan, Factional, Fibonacci, Harmonic, Mersenne Prime, Pascal, Prime, Square, Triangular and Vampire.
Catalan Numbers :-
The Catalan series is the series of derived from the factors of the central numbers from Pascal's Triangle. These are the numbers marked in purple in the diagram below.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1
The Catalan numbers can be explained as below : -
1 = 1 x 1
2 = 2 x 1
6 = 3 x 2
20 = 4 x 5
70 = 5 x 14
Another way of looking at them is that they are Catalan numbers are a binomial series, BINOMIAL [2n, n]/(n + 1). To find the number series 1, 2, 6 20, 70 ... the formula nCr or n! / (n - r)! r! or used. Where to work out the series r increases by 2 and n by 1 for each number in the series. Using the formula n! / (n - r)! r! / (n+1) the Catalan numbers are found. The nth Catalan number counts the ways of dissecting a polygon with n+2 sides into triangles by drawing nonintersecting diagonals.
The series runs 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ...
The program is flawed because of the way QBasic deals with DOUBLE'd numbers. Some numbers aren't calculated to whole numbers and give a lot of decimals. It should be easy enough to spot what the numbers should be.
Factional Series :-
The numbers in this series are the product of the previous numbers multiplied by the position in the series. The common way of writing this is n!
The series runs :- 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800 ... Which is
1 * 1, 1 * 2, 2 * 3, 6 * 4, 24 * 5, 120 * 6, 720 * 7, 5040 * 8, 40320 * 9, 362880 * 10 ...
As you can see this number series gets very big very quickly.
Fibonacci Series :-
Leonardo Fibonacci (Leonardo da Pisa) was born in Pisa, Italy in 1175. He died in 1250.
The series of numbers that he calculated was 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ...
The members of this series are the sum of the previous two numbers. There is another interesting thing about this series. Look at the difference between the numbers. The difference between 2 and 3 is 1, between 3 and 5 is 2, between 5 and 8 is 3 and so on. Ignoring the 0, 1, 1 at the start of the series, the differences between the Fibonacci numbers is another series, it is 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ... Can you see what is happening? The difference between the numbers of the Fibonacci series, is another Fibonacci series.
Harmonic Series :-
This is the series 1 + 1/2 + 1/3 + 1/4 + 1/5 ... 1/n. The series (when factorised) runs ...
1, 3/2, 11/6, 25/12, 137/60, 49/20, 363/140, 761/280, 7129/2520, 7381/2520 ...
The program factorises the numbers it produces, but this slows it down considerably. I've indicated which parts of the Harmon subroutine that can be REM'd out to let it run as quickly as it can. The program also calculates mixed fractions, so that 25/12 becomes 2 1/12. Because this uses the MOD command and some of the numbers used get very big without the factorisation then this part of the code has to be REM'd out too. For an explanation of the MOD problem see the Mersenne Prime section below.
If "C" (test if your number is part of the series) is chosen from the main menu, then the number to be input has to be in the form of a decimal number. One way to allow fractions to be input is to take the input as string. Everything before the / can be taken as the numerator and everything after as the denominator. A simple calculation will turn this back into a decimal so that the comparison in the Harmon subroutine can be made. Suppose the user wants to see if the fraction 12345/6789 is a Harmonic number, using a variable called UserStr$ :-
DIM UserNum AS DOUBLE UserStr$ = "12345/6789" Posn = INSTR(UserStr$, "/") Num = VAL(LEFT$(UserStr$, Posn - 1)) Den = VAL(MID$(UserStr$, Posn + 1)) UserNum = Num / Den
I've also limited the program to only run the Harmon subroutine when "C" is chosen and when the number input is less than 4. This is again due to the factorisation. If a number great than 4 is input the program takes an age to do the calculations. If this code to do this is removed then there is now reason for the limitation on numbers less than 4. However, the program will take a long, long to reach the number that the user input.
Mersenne Prime Numbers :-
This is a prime number series of numbers which is given by 2p - 1, where p is a prime number and so is the Mersenne Prime derived from it. Whilst writing the program I came across a limit of the MOD command in QBasic. The limit is that it only works for numbers less or equal than 2,147,483,647, which is the limit for a long integer, oddly enough this is also a Mersenne Prime. If you've a couple of hours or days you don't mind leaving your computer running you may like to replace the lines
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
that appear in the Mersenne subroutine with the following code
NewNum = (MersTest / MersDiv) * 1000 NewStr$ = STR$(NewNum) IF RIGHT$(NewStr$, 3) = "000" THEN MersPrime = 1
You'll also need to define NewNum as a DOUBLE.
This has the same result as IF MersTest MOD MersDiv = 0 THEN MersPrime = 1 but can deal with very large numbers. The problem is that the program is VERY slow to run. For this reason I've limited the program to calculating the first 8 numbers in the series.
The series is 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 170141183460469231731687303715884105727 ...
These are Mersenne Primes from the normal primes of 2, 3, 5, 7, 13, 17, 19, 31 and 61
Pascal Numbers :-
This is the series of numbers which are the sums of the numbers in each line of Pascal's Triangle. This is a wonderful of construct of numbers in which can be seen the Magic 11's, the Fibonacci sequence, Catalan numbers, Triangular numbers, Square numbers and the polygonal numbers. Although all these number series can be seen, it is very simple.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1
Can you see how it is made? Each number is the sum of the two numbers above and to either side of it, apart from the outside numbers which are always 1. The sum of the rows is very easy to work out. If the top row is called row 0, then for each row the sum of the numbers in that row is 2^row number. In fact the series is just the powers of two ...
1, 2, 4, 8, 16, 32, 64, 128, 256, 512 ...
Perfect Numbers :-
This is the series of numbers which are equal to the sum of all of its positive divisors, excluding itself.
The first in the series is 6 (1+2+3), the second is 28 (1+2+4+7+14)
The series is 6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128, 2658455991569831744654692615953842176, 191561942608236107294793378084303638130997321548169216 ...
Perfect numbers can be calculated by using 2m-1(2m-1) where m is a Mersenne prime number.
As you can see these numbers get very big very quickly, so once again I've limited the number that are generated by the program.
Prime Numbers :-
This is the series of numbers that can only be divided by themselves and 1 (without leaving fractions or a remainder).
The series is 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ...
Square Numbers :-
This is the series of numbers whose square roots are integers (in the mathematical sense, not the programming sense where integers run from -32,768 to +32,767).
The series is 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ...
Can you see the differences in the series? They run 3, 5, 7, 9, 11, 13, 15, 17, 19 ...
There are also cubed (1, 8, 27, 64, 125 ...), quad (1, 16, 81, 256, 625 ...), quint (1, 32, 243, 1024, 3125 ...) numbers and so on.
Triangular Numbers :-
This is the series of numbers that are able to make up a triangle from dots. Perhaps a diagram will make it clearer.
1 o 3 o 6 o 10 o 15 o
o o o o o o o o
o o o o o o o o o
o o o o o o o o
o o o o o
The series is 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ...
Once again there is a series in the difference in the numbers of the series, they run 2, 3, 4, 5, 6, 7, 8, 9 ...
Vampire Numbers :-
Vampire numbers are those numbers that have an even number of digits. The digits can be mixed and split so that each pair of numbers when multiplied together give the vampire number. For example, 1,435 is a vampire number as you can get 35 * 41 from it, so is 2,187 (27 * 81). There are a couple of rules when producing vampire numbers. 150 x 930 = 139,500 (150 * 930) isn't a vampire number because 1395 (15 * 93) IS. The number 125,460 will produce two sets of numbers, 204 * 615 and 246 * 510, but it is only counted once in the series.
The series runs 1260, 1395, 1435, 1530, 1827, 2187, 6880, 102510, 104260, 105210 ... which is
21 * 60, 15 * 93, 35 * 41, 30 * 51, 21 * 87, 27 * 81, 80 * 86, 201 * 510, 260 * 401, 210 * 501 ...
There are two methods of calculating Vampire Numbers.
1) Produce a number and by testing ALL variations of the digits within that number test to see if any combination can produce the initial number. For example take the numbers 1001 to 9999 in turn and test them. Suppose we are up to the number 5678. All the variations for that number are 56*78, 56*87, 57*68, 57*86, 58*67, 58*85, 65*78, 65*87, 67*58, 67*85, 68*57, 68*75, 75*68, 75*86, 76*58, 76*85, 78*67, 78*76, 85*67, 85*76, 86*57, 86*75, 87*56 and 87*65. The work is made slightly easier by the fact we can remove half of these 24 variations, this is because 56*78 is the same as 78*56. This doesn't seem so bad as now we've only 12 possibilities, which can be done using SWAP statements within the program. However, think what happens when we get to 6 digit numbers. We now end up with 720 possible combinations. With that many SWAP statements to write it's probably quicker and more accurate to sit down with pen, paper and calculator and do the sums yourself. One advantage to this method of programming is that the numbers appear smallest to largest. Here's some code to show this method.
VampTest = 1000
Count = 0
ReCurs = 0
VampStr$ = LTRIM$(STR$(VampTest))
VampLen = LEN(LTRIM$(VampStr$))
Fact1 = 0
Fact2 = 0
VampFnd = 0
ReCurs = 0
FOR Count = 1 TO VampLen
VampAry$(Count) = MID$(VampStr$, Count, 1)
NEXT Count
DO
IF VampLen = 4 THEN
IF VampTest MOD 100 = 0 THEN EXIT DO
Div1 = VAL(VampAry$(1) + VampAry$(2))
IF Div1 <> 0 THEN
IF VampTest MOD Div1 = 0 THEN Fact1 = 1
END IF
Div2 = VAL(VampAry$(3) + VampAry$(4))
IF Div2 <> 0 THEN
IF VampTest MOD Div2 = 0 THEN Fact2 = 1
END IF
IF Fact1 = 1 AND Fact2 = 1 THEN
IF Div1 * Div2 = VampTest THEN VampFnd = 1
END IF
IF VampFnd = 0 THEN
ReCurs = ReCurs + 1
SELECT CASE ReCurs
CASE 1
SWAP VampAry$(1), VampAry$(2)
CASE 2
SWAP VampAry$(1), VampAry$(2)
SWAP VampAry$(3), VampAry$(4)
CASE 3
SWAP VampAry$(1), VampAry$(2)
CASE 4
SWAP VampAry$(1), VampAry$(2)
SWAP VampAry$(2), VampAry$(3)
CASE 5
SWAP VampAry$(3), VampAry$(4)
CASE 6
SWAP VampAry$(1), VampAry$(2)
CASE 7
SWAP VampAry$(3), VampAry$(4)
CASE 8
SWAP VampAry$(1), VampAry$(2)
SWAP VampAry$(2), VampAry$(4)
CASE 9
SWAP VampAry$(3), VampAry$(4)
CASE 10
SWAP VampAry$(1), VampAry$(2)
CASE 11
SWAP VampAry$(3), VampAry$(4)
END SELECT
END IF
END IF
LOOP UNTIL ReCurs > 11 OR VampFnd = 1
2) The second method is to multiply a sequence of numbers then see if the product is a Vampire number. The first number only needs to start from 33, 333, 3333 etc. This is because 33 * 10 is only 330, 333 * 100 is only 33300, which are an odd number of digits long. The same can't be done to the second number as 300 * 334 = 102200, then 400 * 250 = 100000, 500 * 200 = 100000, 600 * 167 = 100200, 700 * 143 = 100100, 800 * 125 = 100000 and 900 * 112 = 100800. When the first number reaches 1000, it is increased to 3333 and the second number becomes 1000. The product of these numbers are then tested to see if they are Vampire numbers.
There are a couple of problems with this method.
Some Vampire numbers have spare "fangs", but are only counted as Vampire numbers once. For example 125460 can be produced from 204 * 615 or 246 * 510 but it's only counted once.
The second and more serious is the fact that Vampire numbers are NOT produced in numerical order. The first seven of the series are calculated in the following order 1435, 1530, 1260, 2187, 6880, 1827 and 1395. This is because of the way the numbers are incremented, in fact the order of finding these numbers are 41*35, 51*30, 60*21, 81*27, 80*86, 87*21 and 93*15. Even if these multiples were reversed they still wouldn't give the right order. For this reason the numbers are put into an array and sorted before being displayed.
This leads to another problem, you can't tell if you've got all the Vampire numbers until you've calculated them all for a certain number of digits. For example, if you tell the program to produce the first 10 Vampire numbers, it gives all the 4 digit numbers in the correct order as there are only seven of them. The first three 6 digit Vampire numbers are given as 104260, 135837 and 140350. This is wrong, they should be 102510, 104260 and 105210, but these aren't calculated until positions 26, 9 and 24 respectively. There are 7 Vampire numbers with 4 digits, 148 with 6 digits, 3226 with 8 digits and 108577 with 10 digits, this means to get them all, you need to enter at least 7, 155, 3371 or 111948. I say at least, as don't forget the first problem, some numbers are calculated as Vampire numbers twice.
When using this program remember, the results are only accurate until the next step in the number of digits in the Vampire number is reached. This brings us to yet another problem with this program. Because the QuickSort I've used uses the numbers in an array, and QBasic won't allow more than an arrays longer than 10,000 as a LONG then that's all the numbers it can cope with. The program is therefore only accurate in producing up to 6 digit Vampire numbers.
The program, numser.bas is able to print, within the limits shown under the various sections above, the first part of each of the series, the series up to a number that is input and can check whether a number is part of any of the series. It is able to do this because of the way computer programs can use loops. Because of the length of the program it is at the bottom of the page, after Further Reading.
Further Reading :-
Amazing Number Facts - All sorts of things about numbers
Fibonacci Numbers and the Golden Section - includes easy and hard puzzle pages
GIMPS - Searching for Mersenne Primes
Introduction to Catalan Numbers
Kryss Tal - a good maths site
Largest Known - The largest known Perfect and Prime numbers
Pascal's Triangle and its Patterns
Pascal's Triangle and related triangles
Patterns in Pascal's Triangle *
Perfect Number Journey - Perfect numbers, Primes and Mersenne Primes
Perfect, Amicable and Sociable Numbers
Prime Pages - Perfect numbers, Primes and Mersenne Primes
'Numser.bas Ray Thomas April 2002
OPTION BASE 1
DECLARE SUB Menu ()
DECLARE SUB Catalan ()
DECLARE SUB Facts ()
DECLARE SUB Fibon ()
DECLARE SUB Harmon ()
DECLARE SUB Mersenne ()
DECLARE SUB Pascal ()
DECLARE SUB Perfect ()
DECLARE SUB Primes ()
DECLARE SUB QSort (SortArray() AS LONG, Low AS INTEGER, High AS DOUBLE)
DECLARE SUB Square ()
DECLARE SUB Triang ()
DECLARE SUB Vampire ()
DECLARE SUB Continue ()
DIM SHARED UserIn AS STRING 'User input
DIM SHARED UserNum AS DOUBLE 'User number
DIM SHARED Count AS DOUBLE 'Loop counter
DIM SHARED OldNum AS DOUBLE 'Previous number generated
DO
Menu
Catalan
Continue
Facts
Continue
Fibon
Continue
IF UserIn = "C" AND UserNum < 4 THEN
Harmon
Continue
END IF
Mersenne
Continue
Pascal
Continue
Perfect
Continue
Primes
Continue
Square
Continue
Triang
Continue
Vampire
Continue
LOOP UNTIL UserIn$ = CHR$(27)
END
SUB Catalan
'*** Catalan series ***
DIM Cat AS DOUBLE
DIM Row AS DOUBLE
DIM RowFact AS DOUBLE
DIM Num AS DOUBLE
DIM NumFact AS DOUBLE
DIM NumRow AS DOUBLE
DIM InterMed AS DOUBLE
CLS
PRINT
PRINT "CATALAN NUMBERS"
PRINT
PRINT "Catalan numbers are a binomial series, BINOMIAL [2n, n]/(n + 1)"
PRINT
IF UserIn$ = "A" THEN '*** First n of a series ***
PRINT "These are the first"; UserNum; "Catalan numbers."
PRINT
PRINT 1; '*** I can't calculate this ***
Row = 0
Num = 0
FOR Count = 1 TO UserNum
Num = Num + 1
Row = Row + 2
NumFact = 1
RowFact = 1
NumRow = 1
'*** Calculate the factorials ***
FOR Counter = 1 TO Num
NumFact = NumFact * Counter
NEXT Counter
FOR Counter = 1 TO Row
RowFact = RowFact * Counter
NEXT Counter
FOR Counter = 1 TO Row - Num
NumRow = NumRow * Counter
NEXT Counter
'*** Do the sums ***
'*** Intermed is the series from Pascal's Triangle ***
'*** 1, 2, 6, 20, 70 ... ***
InterMed = RowFact / (NumFact * NumRow)
Cat = InterMed / (Num + 1)
PRINT Cat;
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Series up to a number ***
PRINT "These are the Catalan numbers up to"; UserNum
PRINT
PRINT 1; '*** I can't calculate this ***
Row = 0
Num = 0
Count = 1
DO
Num = Num + 1
Row = Row + 2
NumFact = 1
RowFact = 1
NumRow = 1
'*** Calculate the factorials ***
FOR Counter = 1 TO Num
NumFact = NumFact * Counter
NEXT Counter
FOR Counter = 1 TO Row
RowFact = RowFact * Counter
NEXT Counter
FOR Counter = 1 TO Row - Num
NumRow = NumRow * Counter
NEXT Counter
'*** Do the sums ***
'*** Intermed is the series from Pascal's Triangle ***
'*** 1, 2, 6, 20, 70 ... ***
InterMed = RowFact / (NumFact * NumRow)
Cat = InterMed / (Num + 1)
PRINT Cat;
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Cat >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Catalan numbers less than or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number in a series? ***
Row = 0
Num = 0
Count = 1
DO
Num = Num + 1
Row = Row + 2
NumFact = 1
RowFact = 1
NumRow = 1
OldNum = Cat
'*** Calculate the factorials ***
FOR Counter = 1 TO Num
NumFact = NumFact * Counter
NEXT Counter
FOR Counter = 1 TO Row
RowFact = RowFact * Counter
NEXT Counter
FOR Counter = 1 TO Row - Num
NumRow = NumRow * Counter
NEXT Counter
'*** Do the sums ***
'*** Intermed is the series from Pascal's Triangle ***
'*** 1, 2, 6, 20, 70 ... ***
InterMed = RowFact / (NumFact * NumRow)
Cat = InterMed / (Num + 1)
Count = Count + 1
LOOP UNTIL Cat >= UserNum
IF Cat = UserNum THEN
PRINT UserNum; "is a Catalan number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a Catalan number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Catalan number is"; Cat
END IF
END IF
END SUB
SUB Continue
'*** Press any key to continue ***
PRINT
PRINT
PRINT "Press any key to continue ..."
DO
LOOP UNTIL INKEY$ <> ""
PRINT
END SUB
SUB Facts
'*** Factorials ***
DIM Fact AS DOUBLE
DIM NewMax AS DOUBLE
NewMax = UserNum
IF UserNum > 169 THEN NewMax = 169
CLS
PRINT
PRINT "FACTORIAL NUMBERS"
PRINT
PRINT "Factorial numbers are the product of the numbers 1 to n"
PRINT
PRINT "These numbers get very big very quckly"
PRINT
IF UserIn$ = "A" THEN '*** First n of a series ***
PRINT "These are the first"; NewMax; "factorial numbers."
PRINT
Fact = 1
FOR Count = 0 TO NewMax
Fact = Fact + (Fact * Count)
PRINT Fact;
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Series up to a number ***
PRINT "These are factorial numbers up to"; UserNum
PRINT
Fact = 1
Count = 0
DO
Fact = Fact + (Fact * Count)
IF Fact > UserNum THEN EXIT DO
PRINT Fact;
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Fact >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "factorials under or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number in a series? ***
Fact = 1
Count = 0
DO
OldNum = Fact
Fact = Fact + (Fact * Count)
Count = Count + 1
LOOP UNTIL Fact >= UserNum
IF Fact = UserNum THEN
PRINT UserNum; "is a Factorial"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a factorial"
PRINT
PRINT "The next smallest number is"; OldNum; "the next factorial is"; Fact
END IF
END IF
END SUB
SUB Fibon
'*** Fibonacci numbers ***
DIM Num AS DOUBLE
DIM SumNum AS DOUBLE
DIM NewNum AS DOUBLE
CLS
PRINT
PRINT "FIBONACCI NUMBERS"
PRINT
PRINT "Fibonacci numbers are the series of numbers where the next number generated"
PRINT "is the sum of the previous two numbers."
PRINT
PRINT "These numbers get very big very quckly"
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "The first"; UserNum; "numbers in the Fibonacci series are :-"
PRINT
SumNum = 0
OldNum = 0
NewNum = 1
Count = 0
DO
PRINT SumNum;
SumNum = OldNum + NewNum
NewNum = OldNum
OldNum = SumNum
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Count = UserNum
END IF
IF UserIn$ = "B" THEN '*** Series up to a number ***
PRINT "The Fibonacci series up to and including"; UserNum; "are :-"
PRINT
SumNum = 0
OldNum = 0
NewNum = 1
Count = 0
DO
PRINT SumNum;
SumNum = OldNum + NewNum
NewNum = OldNum
OldNum = SumNum
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL SumNum >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Fibonacci numbers under or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number in a series? ***
SumNum = 0
OldNum = 0
NewNum = 1
Count = 0
DO
OldNum = SumNum
SumNum = OldNum + NewNum
NewNum = OldNum
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL SumNum >= UserNum
IF SumNum = UserNum THEN
PRINT UserNum; "is a Fibonacci number"
PRINT
PRINT "It is"; Count + 1; "in the series"
ELSE
PRINT UserNum; "is not a Fibonacci number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Fabonacci number is"; SumNum
END IF
END IF
END SUB
SUB Harmon
DIM HarmDen AS DOUBLE 'Harmonic denominator
DIM HarmNum AS DOUBLE 'Harmonic numerator
DIM HarmSum AS DOUBLE 'The sum of the series, as a decimal
DIM NewDen AS DOUBLE 'Next denominator
DIM NewNum AS DOUBLE 'Next numerator to be added
DIM CmnDen AS DOUBLE 'Common denominator
DIM WholeNum AS INTEGER 'Integer part of numerator / denominator
DIM Counter AS LONG 'Loop counter
DIM OldDen AS DOUBLE 'Old denominator
DIM Harm AS DOUBLE 'Result of numerator / denominator
CLS
PRINT
PRINT "HARMONIC NUMBERS"
PRINT
PRINT "Harmonic numbers are the series 1 + 1/2 + 1/3 + 1/4 + 1/5 etc. to 1/n"
PRINT
IF UserIn$ = "A" THEN '*** First n of a series ***
PRINT "These are the first"; UserNum; "Harmonic numbers."
PRINT
PRINT 1
HarmDen = 1
HarmNum = 1
NewDen = 1
CmnDen = 0
FOR Count = 2 TO UserNum
NewDen = NewDen + 1
CmnDen = HarmDen * NewDen
HarmNum = HarmNum * NewDen
NewNum = HarmDen
HarmNum = HarmNum + NewNum
HarmDen = CmnDen
PRINT STR$(HarmNum); "/"; LTRIM$(STR$(HarmDen));
'*** To improve the speed of the program REM (or use ') ***
'*** From the line below to the line '*********************
'*** Factorise the Harmonic fraction ***
FOR Counter = HarmDen TO 2 STEP -1
IF HarmNum MOD Counter = 0 AND HarmDen MOD Counter = 0 THEN
HarmNum = HarmNum / Counter
HarmDen = HarmDen / Counter
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
IF HarmNum MOD 2 = 0 AND HarmDen MOD 2 = 0 THEN
HarmNum = HarmNum / 2
HarmDen = HarmDen / 2
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
NEXT Counter
'*** Produce a mixed number ***
WholeNum = INT(HarmNum / HarmDen)
PRINT " ="; WholeNum; LTRIM$(STR$(HarmNum MOD HarmDen)); "/"; LTRIM$(STR$(HarmDen));
'**********************************************************
PRINT " ="; HarmNum / HarmDen
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Harmonic series up to and including a number ***
PRINT "These are Harmonic numbers up to"; UserNum
PRINT
PRINT 1
HarmDen = 1
HarmNum = 1
NewDen = 1
CmnDen = 0
Count = 0
DO
NewDen = NewDen + 1
CmnDen = HarmDen * NewDen
HarmNum = HarmNum * NewDen
NewNum = HarmDen
HarmNum = HarmNum + NewNum
HarmDen = CmnDen
Count = Count + 1
IF HarmNum / HarmDen > UserNum THEN EXIT DO
PRINT STR$(HarmNum); "/"; LTRIM$(STR$(HarmDen));
'*** To improve the speed of the program REM (or use ') ***
'*** From the line below to the line '*********************
'*** Factorise the Harmonic fraction ***
FOR Counter = HarmDen TO 2 STEP -1
IF HarmNum MOD Counter = 0 AND HarmDen MOD Counter = 0 THEN
HarmNum = HarmNum / Counter
HarmDen = HarmDen / Counter
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
IF HarmNum MOD 2 = 0 AND HarmDen MOD 2 = 0 THEN
HarmNum = HarmNum / 2
HarmDen = HarmDen / 2
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
NEXT Counter
'*** Produce a mixed number ***
WholeNum = INT(HarmNum / HarmDen)
PRINT " ="; WholeNum; LTRIM$(STR$(HarmNum MOD HarmDen)); "/"; LTRIM$(STR$(HarmDen));
'**********************************************************
PRINT " ="; HarmNum / HarmDen
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL HarmNum / HarmDen >= UserNum
PRINT
PRINT "There are"; Count; "Harmonic numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number in the Harmonic series? ***
HarmDen = 1
HarmNum = 1
NewDen = 1
CmnDen = 0
Count = 1
OldNum = 0
OldDen = 0
DO
OldNum = HarmNum
OldDen = HarmDen
NewDen = NewDen + 1
CmnDen = HarmDen * NewDen
HarmNum = HarmNum * NewDen
NewNum = HarmDen
HarmNum = HarmNum + NewNum
HarmDen = CmnDen
Count = Count + 1
Harm = HarmNum / HarmDen
LOOP UNTIL Harm >= UserNum
'*** To improve the speed of the program REM (or use ') ***
'*** From the line below to the line '*********************
IF Harm = UserNum THEN
PRINT UserNum; "is a Harmonic Number"
PRINT
PRINT "It is"; Count; "in the series"
PRINT
PRINT STR$(HarmNum); "/"; LTRIM$(STR$(HarmDen));
ELSE
PRINT UserNum; "is not a Harmonic number."
PRINT
PRINT "The next smallest number is"; STR$(OldNum); "/"; LTRIM$(STR$(OldDen));
SWAP OldNum, HarmNum
SWAP OldDen, HarmDen
END IF
'*** To improve the speed of the program REM (or use ') ***
'*** From the line below to the line '*********************
'*** Factorise the Harmonic fraction ***
FOR Counter = HarmDen TO 2 STEP -1
IF HarmNum MOD Counter = 0 AND HarmDen MOD Counter = 0 THEN
HarmNum = HarmNum / Counter
HarmDen = HarmDen / Counter
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
IF HarmNum MOD 2 = 0 AND HarmDen MOD 2 = 0 THEN
HarmNum = HarmNum / 2
HarmDen = HarmDen / 2
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
NEXT Counter
'*** Produce a mixed number ***
WholeNum = INT(HarmNum / HarmDen)
PRINT " ="; WholeNum; LTRIM$(STR$(HarmNum MOD HarmDen)); "/"; LTRIM$(STR$(HarmDen));
'**********************************************************
PRINT " ="; HarmNum / HarmDen
IF Harm > UserNum THEN
SWAP OldNum, HarmNum
SWAP OldDen, HarmDen
PRINT
PRINT "The next largest is"; STR$(HarmNum); "/"; LTRIM$(STR$(HarmDen));
'*** To improve the speed of the program REM (or use ') ***
'*** From the line below to the line '*********************
'*** Factorise the Harmonic fraction ***
FOR Counter = HarmDen TO 2 STEP -1
IF HarmNum MOD Counter = 0 AND HarmDen MOD Counter = 0 THEN
HarmNum = HarmNum / Counter
HarmDen = HarmDen / Counter
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
IF HarmNum MOD 2 = 0 AND HarmDen MOD 2 = 0 THEN
HarmNum = HarmNum / 2
HarmDen = HarmDen / 2
PRINT " = "; LTRIM$(STR$(HarmNum)); "/"; LTRIM$(STR$(HarmDen));
END IF
NEXT Counter
'*** Produce a mixed number ***
WholeNum = INT(HarmNum / HarmDen)
PRINT " ="; WholeNum; LTRIM$(STR$(HarmNum MOD HarmDen)); "/"; LTRIM$(STR$(HarmDen));
'********************************************************
PRINT " ="; HarmNum / HarmDen
END IF
END IF
END SUB
SUB Menu
'*** Introduction and menu to the program ***
CLS
PRINT
PRINT " This program is an introduction to number series."
PRINT
PRINT " The series this program can calculate are :-"
PRINT
PRINT " Factorials, Fibonacci, Mersenne Primes, Pascal, Perfect, Primes,"
PRINT " Squares, Triangular and Vampire."
PRINT
PRINT
PRINT
PRINT " Choose what you want the program to do :-"
PRINT
PRINT
PRINT " A = The first n numbers of the series."
PRINT
PRINT " B = The series up to and including your number."
PRINT
PRINT " C = Test if your number is part of the series."
PRINT
PRINT " Esc = Exit Program"
PRINT
DO
UserIn$ = UCASE$(INKEY$)
LOOP UNTIL INSTR(" ABC", UserIn$) > 1 OR UserIn$ = CHR$(27)
IF UserIn$ = CHR$(27) THEN END
PRINT
PRINT
PRINT " There are limits to the size of the numbers that can be displayed :-"
PRINT
PRINT " First 169 only in the Factorial series, first 8 only in Mersenne Primes"
PRINT " and Perfect numbers, 6 digit Vampire numbers etc."
PRINT
INPUT ; " What is your number"; UserNum
PRINT
END SUB
SUB Mersenne
'*** Mersenne Prime Numbers ***
DIM TestNum AS DOUBLE 'TestNum the number being tested
DIM Prime AS INTEGER 'Switch to indicate a prime during testing
DIM Divisor AS LONG 'Holds divisors
DIM MersTest AS DOUBLE 'Mersenne test numbers
DIM MersDiv AS DOUBLE 'Holds Mersenne divisors
DIM MersPrime AS INTEGER 'Switch to indicate a Mersenne Prime
Divisor = 2
Count = 2
CLS
PRINT
PRINT "MERSENNE PRIME NUMBERS"
PRINT
PRINT "Mersenne Prime numbers are those that take the form (2^p) - 1"
PRINT
PRINT "Where p and the Mersenne number produced are prime numbers"
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "Here are the first"; UserNum; "Mersenne Prime numbers."
PRINT
PRINT 3; 7; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
IF MersPrime = 0 THEN
Count = Count + 1
PRINT MersTest;
END IF
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Count = UserNum
END IF
IF UserIn$ = "B" THEN '*** Mersenne Prime numbers up to and including a number ***
PRINT "Here are the Mersenne Prime numbers up to or equal to"; UserNum
PRINT
PRINT 3; 7; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest > UserNum THEN
MersPrime = 1
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
IF MersPrime = 0 THEN
Count = Count + 1
PRINT MersTest;
END IF
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL MersTest >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Mersenne Prime numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number is part of the series? ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
IF MersPrime = 0 THEN
Count = Count + 1
IF MersTest >= UserNum THEN EXIT DO
IF MersTest < UserNum THEN OldNum = MersTest
END IF
END IF
LOOP UNTIL MersPrime = 0 AND MersTest >= UserNum
IF MersTest = UserNum THEN
PRINT UserNum; "is a Mersenne Prime number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a Mersenne Prime number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Mersenne Prime number is"; MersTest
END IF
END IF
END SUB
SUB Pascal
'*** Pascal Numbers ***
DIM PascNum AS DOUBLE
CLS
PRINT
PRINT "PASCAL NUMBERS"
PRINT
PRINT "Pascal numbers are the sum of the numbers in each row of Pascal's Triangle"
PRINT
IF UserIn$ = "A" THEN '*** First n of a series ***
PRINT "These are the first"; UserNum; "Pascal numbers."
PRINT
FOR Count = 0 TO UserNum - 1
PascNum = 2 ^ Count
PRINT PascNum;
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Series up to a number ***
PRINT "These are Pascal numbers up to"; UserNum
PRINT
PascNum = 0
Count = 0
DO
PascNum = 2 ^ Count
IF PascNum > UserNum THEN EXIT DO
PRINT PascNum;
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Fact >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Pascal less than or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number in a series? ***
PascNum = 0
Count = 0
DO
OldNum = PascNum
PascNum = 2 ^ Count
Count = Count + 1
LOOP UNTIL PascNum >= UserNum
IF Fact = UserNum THEN
PRINT UserNum; "is a Pascal number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a Pascal number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Pascal number is"; PascNum
END IF
END IF
END SUB
SUB Perfect
'*** Perfect Numbers ***
DIM TestNum AS DOUBLE 'TestNum the number being tested
DIM Prime AS INTEGER 'Switch to indicate a prime during testing
DIM Divisor AS LONG 'Holds divisors
DIM MersTest AS DOUBLE 'Mersenne test numbers
DIM MersDiv AS DOUBLE 'Holds Mersenne divisors
DIM MersPrime AS INTEGER 'Switch to indicate a Mersenne Prime
DIM Perf AS DOUBLE 'Perfect Numbers
Divisor = 2
Count = 2
CLS
PRINT
PRINT "PERFECT NUMBERS"
PRINT
PRINT "Perfect numbers are those whose positive divisors (except for"
PRINT "itself) sum to itself. It is also a function of Mersenne Primes"
PRINT "using (2^m-1)((2^m)-1)"
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "Here are the first"; UserNum; "Perfect numbers."
PRINT
PRINT 6; 28; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Perf = 0
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
'*** Now calculate the Perfect number ***
IF MersPrime = 0 THEN
Count = Count + 1
Perf = (2 ^ (TestNum - 1)) * MersTest
PRINT Perf;
END IF
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Count = UserNum
END IF
IF UserIn$ = "B" THEN '*** Perfect numbers up to and including a number ***
PRINT "Here are the Perfect numbers up to or equal to"; UserNum
PRINT
PRINT 6; 28; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Prime = 0
Perf = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
IF MersPrime = 0 THEN
Perf = (2 ^ (TestNum - 1)) * MersTest
IF Perf > UserNum THEN EXIT DO
PRINT Perf;
Count = Count + 1
END IF
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Perf >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Perfect numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number is part of the series? ***
TestNum = 3
Count = 2
DO
'*** First of all find the Prime Numbers ***
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
'*** Now we've got a Prime, calculate the Mersenne Prime ***
IF Prime = 0 THEN
MersTest = (2 ^ TestNum) - 1
'*** Now test if MersTest is a Prime ***
MersPrime = 0
MersDiv = 3
DO
IF MersTest > 2147483647 THEN
PRINT
PRINT
PRINT "Routine aborted, MOD can't cope with big numbers !!!"
MersPrime = 1
Count = UserNum
EXIT DO
END IF
IF MersTest MOD MersDiv = 0 THEN MersPrime = 1
MersDiv = MersDiv + 2
IF MersDiv > SQR(MersTest) THEN EXIT DO
LOOP UNTIL MersPrime = 1
IF MersPrime = 0 THEN
Perf = (2 ^ (TestNum - 1)) * MersTest
Count = Count + 1
IF Perf >= UserNum THEN EXIT DO
IF Perf < UserNum THEN OldNum = Perf
END IF
END IF
LOOP UNTIL MersPrime = 0 AND Perf >= UserNum
IF Perf = UserNum THEN
PRINT UserNum; "is a Perfect number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a Perfect number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Perfect number is"; Perf
END IF
END IF
END SUB
SUB Primes
'*** Prime Numbers ***
DIM TestNum AS LONG 'TestNum the number being tested
DIM Prime AS INTEGER 'Switch to indicate a prime during testing
DIM Divisor AS LONG 'Holds divisors
Divisor = 2
Count = 2
CLS
PRINT
PRINT "PRIME NUMBERS"
PRINT
PRINT "Prime numbers are those that are only divisible by themselves or 1"
PRINT
PRINT "The program can calculate the primes up to 1 million in around 90 seconds"
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "Here are the first"; UserNum; "Prime numbers."
PRINT
PRINT 2; 3; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
IF Prime = 0 THEN
PRINT TestNum;
Count = Count + 1
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Count = UserNum
END IF
IF UserIn$ = "B" THEN '*** Prime numbers up to and including a number ***
PRINT "Here are the Prime numbers up to or equal to"; UserNum
PRINT
PRINT 2; 3; '*** I can't find a way of calculating these ***
TestNum = 3
Count = 2
DO
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
IF Prime = 0 THEN
IF TestNum > UserNum THEN EXIT DO
PRINT TestNum;
Count = Count + 1
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL TestNum >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Prime numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number is part of the series? ***
TestNum = 3
Count = 2
DO
Prime = 0
Divisor = 3
TestNum = TestNum + 2
DO
IF TestNum MOD Divisor = 0 THEN Prime = 1
Divisor = Divisor + 2
IF Divisor > SQR(TestNum) THEN EXIT DO
LOOP UNTIL Prime = 1
IF Prime = 0 THEN
Count = Count + 1
IF TestNum >= UserNum THEN EXIT DO
IF TestNum < UserNum THEN OldNum = TestNum
END IF
LOOP UNTIL Prime = 0 AND TestNum >= UserNum
IF TestNum = UserNum THEN
PRINT UserNum; "is a Prime number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a Prime number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next Prime number is"; TestNum
END IF
END IF
END SUB
SUB QSort (SortArray() AS LONG, Low AS INTEGER, High AS DOUBLE)
DIM Lower AS INTEGER
DIM Higher AS INTEGER
DIM RandIndex AS INTEGER
DIM Partition AS DOUBLE
'QuickSort works by picking a random "pivot" element in SortArray, then
'moving every element that is bigger to one side of the pivot, and every
'element that is smaller to the other side. QuickSort is then called
'recursively with the two subdivisions created by the pivot. Once the
'number of elements in a subdivision reaches two, the recursive calls end
'and the array is sorted.
IF Low < High THEN
' *** Only two elements in this subdivision ***
' *** Swap them if they are out of order, then end recursive calls: ***
IF High - Low = 1 THEN
IF SortArray(Low) > SortArray(High) THEN
SWAP SortArray(Low), SortArray(High)
END IF
ELSE
'*** Pick a pivot element at random, then move it to the end ***
RandIndex = INT(RND * (High - Low + 1)) + Low
SWAP SortArray(High), SortArray(RandIndex)
Partition = SortArray(High)
DO
'*** Move in from both sides towards the pivot element ***
Lower = Low
Higher = High
DO WHILE (Lower < Higher) AND (SortArray(Lower) <= Partition)
Lower = Lower + 1
LOOP
DO WHILE (Higher > Lower) AND (SortArray(Higher) >= Partition)
Higher = Higher - 1
LOOP
'*** If pivot element not reached, it means that ***
'*** two elements on either side are out of order, ***
'*** so swap them ***
IF Lower < Higher THEN
SWAP SortArray(Lower), SortArray(Higher)
END IF
LOOP WHILE Lower < Higher
'*** Move the pivot element back to its proper place in the array ***
SWAP SortArray(Lower), SortArray(High)
'*** Recursively call the SortArray sub ***
'*** Pass the smaller subdivision first to use less stack space ***
IF (Lower - Low) < (High - Lower) THEN
QSort SortArray(), Low, Lower - 1
QSort SortArray(), Lower + 1, High
ELSE
QSort SortArray(), Lower + 1, High
QSort SortArray(), Low, Lower - 1
END IF
END IF
END IF
END SUB
SUB Square
'*** Square numbers ***
DIM SqrNum AS LONG 'Square number
CLS
PRINT
PRINT "SQUARE NUMBERS"
PRINT
PRINT "Square numbers are those whose square roots are an interger "
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "These are the first"; UserNum; "square numbers."
PRINT
SqrNum = 0
FOR Count = 1 TO UserNum
SqrNum = SqrNum + 1
PRINT SqrNum * SqrNum;
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Square numbers up to a number ***
PRINT "These are the Square Numbers smaller or equal to"; UserNum
PRINT
SqrNum = 0
Count = 0
DO
SqrNum = SqrNum + 1
IF SqrNum * SqrNum > UserNum THEN EXIT DO
PRINT SqrNum * SqrNum;
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL SqrNum * SqrNum >= UserNum
PRINT
PRINT
PRINT "There are"; Count; "Square Numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** Number is a square number? ***
SqrNum = 0
Count = 0
DO
OldNum = SqrNum * SqrNum
SqrNum = SqrNum + 1
IF SqrNum * SqrNum > UserNum THEN EXIT DO
Count = Count + 1
LOOP UNTIL SqrNum * SqrNum >= UserNum
IF SqrNum * SqrNum = UserNum THEN
PRINT UserNum; "is a square number"
PRINT
PRINT "It is"; Count; "in the series"
ELSE
PRINT UserNum; "is not a square number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next square number is"; SqrNum * SqrNum
END IF
END IF
END SUB
SUB Triang
'*** Triangular numbers ***
DIM Tri AS LONG 'The triangular number
CLS
PRINT
PRINT "TRINGULAR NUMBERS"
PRINT
PRINT "Triangular numbers are a type of arithmetic progression"
PRINT
IF UserIn$ = "A" THEN '*** First n of the series ***
PRINT "These are the first"; UserNum; "triangular numbers."
PRINT
Tri = 0
FOR Count = 1 TO UserNum
Tri = Tri + Count
PRINT Tri;
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
END IF
IF UserIn$ = "B" THEN '*** Triangular numbers smaller or equal to UserNum ***
PRINT "These are triangular numbers smaller or equal to"; UserNum
PRINT
Tri = 0
Count = 1
DO
Tri = Tri + Count
IF Tri > UserNum THEN EXIT DO
PRINT Tri;
Count = Count + 1
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
LOOP UNTIL Tri >= UserNum
PRINT
PRINT
PRINT "There are"; Count - 1; "triangular numbers smaller or equal to"; UserNum
END IF
IF UserIn$ = "C" THEN '*** UserNum is a triangular number? ***
Tri = 0
Count = 1
DO
OldNum = Tri
Tri = Tri + Count
IF Tri > UserNum THEN EXIT DO
Count = Count + 1
LOOP UNTIL Tri >= UserNum
IF Tri = UserNum THEN
PRINT UserNum; "is a triangular number"
PRINT
PRINT "It is"; Count - 1; "in the series"
ELSE
PRINT UserNum; "is not a triangular number"
PRINT
PRINT "The next smallest number is"; OldNum; "the next triangular number is"; Tri
END IF
END IF
END SUB
SUB Vampire
DIM VampAry(10000) AS LONG 'Aray to hold Vampire numbers for sorting
DIM VampTest AS DOUBLE 'Number to test
DIM VampStr AS STRING 'String to hold VampTest
DIM VampCnt AS DOUBLE 'Number of vampire numbers produced
DIM Div1 AS LONG 'First divisor
DIM Div2 AS LONG 'Second divisor
DIM VampFnd AS INTEGER 'Vampire number found
DIM DivStr AS STRING 'String to hold Div1 and Div2
DIM Div1Str AS STRING 'String to hold Div1
DIM Div2Str AS STRING 'String to hold Div2
DIM DivChar AS STRING * 1 'String to hold individual characters from DivStr$
DIM DivFnd AS INTEGER 'Character position of DivChar$ in VampStr$
DIM Div1Strt AS LONG 'Start number for Div1
DIM Div2Strt AS LONG 'Start number for Div2
DIM UniqVamp AS INTEGER 'Unique Vampire numbers produced
DIM LastVamp AS LONG 'The last found Vampire number
CLS
PRINT
PRINT "VAMPIRE NUMBERS"
PRINT
PRINT "Vampire numbers are numbers with an even number of digits. When mixed and"
PRINT "each pair of numbers when multiplied together give the vampire number."
PRINT
PRINT "The results are only accurate until the next step in the number of digits"
PRINT "in the Vampire number is reached."
PRINT
IF UserIn$ = "A" THEN '*** First n of a series ***
PRINT "These are the first"; UserNum; "CALCULATED Vampire numbers."
PRINT
Div1 = 33
VampFnd = 0
Div1Strt = 33
Div2Strt = 10
VampCnt = 0
UniqVamp = 0
DO
'*** Div1 does not have to start from 10, 100, 1000 etc. ***
'*** It needs to start at 33, 333, 3333 etc. ***
'*** Ensure that Div1 and Div2 are of equal length ***
'*** If Div1 = 333, Div2 = 100, if Div1 = 3333, Div2 = 1000 etc. ***
IF LEN(LTRIM$(STR$(Div1))) > LEN(LTRIM$(STR$(Div1Strt))) THEN
Div1Strt = (Div1Strt * 10) + 3
Div1 = Div1Strt
Div2Strt = Div2Strt * 10
END IF
Div2 = Div2Strt
DO
VampFnd = 0
VampTest = Div1 * Div2
'*** Test VampTest for being a Vampire Number ***
VampStr$ = LTRIM$(STR$(VampTest))
IF Div1 MOD 10 = 0 AND Div2 MOD 10 = 0 THEN VampFnd = 1
IF LEN(VampStr$) MOD 2 <> 0 THEN VampFnd = 1
DivStr$ = LTRIM$(STR$(Div1)) + LTRIM$(STR$(Div2))
'*** Test to see if the Div numbers are part of VampTest ***
FOR Count = 1 TO LEN(DivStr$)
DivChar$ = MID$(DivStr$, Count, 1)
DivFnd = INSTR(VampStr$, DivChar$)
IF DivFnd > 0 THEN
MID$(VampStr$, DivFnd, 1) = "X"
ELSE
VampFnd = 1
END IF
NEXT Count
'*** If VampFnd = 0 then VampTest is a Vampire Number ***
IF VampFnd = 0 THEN
VampCnt = VampCnt + 1
VampAry(VampCnt) = VampTest
END IF
Div2 = Div2 + 1
LOOP UNTIL Div2 > Div1
Div1 = Div1 + 1
LOOP UNTIL VampCnt >= UserNum
'*** The Vampire numbers produced need to be sorted ***
'*** and the duplicates discarded ***
QSort VampAry(), 1, VampCnt
FOR Count = 1 TO VampCnt
IF VampAry(Count + 1) <> VampAry(Count) THEN
PRINT VampAry(Count);
UniqVamp = UniqVamp + 1
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
PRINT
PRINT
PRINT "The sequence contains"; UniqVamp; "Vampire numbers."
PRINT "There were"; VampCnt - UniqVamp; "discarded duplicates."
END IF
IF UserIn$ = "B" THEN '*** Calculated numbers up to and including UserNum ***
PRINT "Here are the CALCULATED Vampire numbers up to or equal to"; UserNum
PRINT
Div1 = 33
VampFnd = 0
Div1Strt = 33
Div2Strt = 10
UniqVamp = 0
VampCnt = 0
DO
'*** Div1 does not have to start from 10, 100, 1000 etc. ***
'*** It needs to start at 33, 333, 3333 etc. ***
'*** Ensure that Div1 and Div2 are of equal length ***
'*** If Div1 = 333, Div2 = 100, if Div1 = 3333, Div2 = 1000 etc. ***
IF LEN(LTRIM$(STR$(Div1))) > LEN(LTRIM$(STR$(Div1Strt))) THEN
Div1Strt = (Div1Strt * 10) + 3
Div1 = Div1Strt
Div2Strt = Div2Strt * 10
END IF
Div2 = Div2Strt
DO
VampFnd = 0
VampTest = Div1 * Div2
'*** Test VampTest for being a Vampire Number ***
VampStr$ = LTRIM$(STR$(VampTest))
IF Div1 MOD 10 = 0 AND Div2 MOD 10 = 0 THEN VampFnd = 1
IF LEN(VampStr$) MOD 2 <> 0 THEN VampFnd = 1
DivStr$ = LTRIM$(STR$(Div1)) + LTRIM$(STR$(Div2))
'*** Test to see if the Div numbers are part of VampTest ***
FOR Count = 1 TO LEN(DivStr$)
DivChar$ = MID$(DivStr$, Count, 1)
DivFnd = INSTR(VampStr$, DivChar$)
IF DivFnd > 0 THEN
MID$(VampStr$, DivFnd, 1) = "X"
ELSE
VampFnd = 1
END IF
NEXT Count
'*** If VampFnd = 0 then VampTest is a Vampire Number ***
IF VampFnd = 0 THEN
VampCnt = VampCnt + 1
VampAry(VampCnt) = VampTest
END IF
Div2 = Div2 + 1
LOOP UNTIL Div2 > Div1
Div1 = Div1 + 1
LOOP UNTIL VampTest >= UserNum
'*** The Vampire numbers produced need to be sorted ***
'*** and the duplicates discarded ***
QSort VampAry(), 1, VampCnt
FOR Count = 1 TO VampCnt
IF VampAry(Count + 1) <> VampAry(Count) THEN
PRINT VampAry(Count);
UniqVamp = UniqVamp + 1
END IF
IF CSRLIN > 19 THEN
Continue
CLS
PRINT
END IF
NEXT Count
PRINT
PRINT
PRINT "There are"; UniqVamp; "CALCULATED Vampire numbers smaller or equal to"; UserNum
PRINT "There were"; VampCnt - UniqVamp; "discarded duplicates."
END IF
IF UserIn$ = "C" THEN '*** Number is part of the series? ***
Div1 = 33
VampFnd = 0
Div1Strt = 33
Div2Strt = 10
DO
'*** Div1 does not have to start from 10, 100, 1000 etc. ***
'*** It needs to start at 33, 333, 3333 etc. ***
'*** Ensure that Div1 and Div2 are of equal length ***
'*** If Div1 = 333, Div2 = 100, if Div1 = 3333, Div2 = 1000 etc. ***
IF LEN(LTRIM$(STR$(Div1))) > LEN(LTRIM$(STR$(Div1Strt))) THEN
Div1Strt = (Div1Strt * 10) + 3
Div1 = Div1Strt
Div2Strt = Div2Strt * 10
END IF
Div2 = Div2Strt
DO
VampFnd = 0
VampTest = Div1 * Div2
'*** Test VampTest for being a Vampire Number ***
VampStr$ = LTRIM$(STR$(VampTest))
IF Div1 MOD 10 = 0 AND Div2 MOD 10 = 0 THEN VampFnd = 1
IF LEN(VampStr$) MOD 2 <> 0 THEN VampFnd = 1
DivStr$ = LTRIM$(STR$(Div1)) + LTRIM$(STR$(Div2))
'*** Test to see if the Div numbers are part of VampTest ***
FOR Count = 1 TO LEN(DivStr$)
DivChar$ = MID$(DivStr$, Count, 1)
DivFnd = INSTR(VampStr$, DivChar$)
IF DivFnd > 0 THEN
MID$(VampStr$, DivFnd, 1) = "X"
ELSE
VampFnd = 1
END IF
NEXT Count
'*** If VampFnd = 0 then VampTest is a Vampire Number ***
IF VampFnd = 0 THEN
VampCnt = VampCnt + 1
VampAry(VampCnt) = VampTest
LastVamp = VampTest
END IF
Div2 = Div2 + 1
LOOP UNTIL Div2 > Div1
Div1 = Div1 + 1
LOOP UNTIL LastVamp > UserNum
'*** The Vampire numbers produced need to be sorted ***
'*** and the duplicates discarded ***
QSort VampAry(), 1, VampCnt
Count = 0
DO
Count = Count + 1
IF VampAry(Count + 1) <> VampAry(Count) THEN UniqVamp = UniqVamp + 1
LOOP UNTIL VampAry(Count) >= UserNum
IF VampAry(Count) = UserNum THEN
PRINT VampAry(Count); "is a Vampire Number,"
PRINT
PRINT "it is"; Count - (UniqVamp - Count); "in the CALCULATED series"
ELSE
PRINT UserNum; "is not a CALCULATED Vampire number,"
PRINT
IF Count > 1 THEN
PRINT "the next smallest CALCULATED number is"; VampAry(Count - 1);
PRINT
END IF
PRINT "the next largest CALCULATED Vampire number is"; VampAry(Count)
END IF
END IF
END SUB
The programs on this page, like all the programs written for this site, can be downloaded from the DLoad page.
QBasic | Errors | 40lb Weight | Bits | Chance | Colours | Dates | Delays | File Dialog | Files | Input | Matching | Menus | Mouse | Numbers | SeqNo | SIRDS | Sorts | Text | Timer | DLoads
HomePage | Optical Illusions | War Stories | QBasic | Dads Navy Days | Bristol | Bristol, USA | Bristol, Canada | Terre Haute | Miscellany | Web Stuff | About Ray | Site Map | Site Search | Messages | Credits | Links | Web Rings